|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
10/09/24 06:22
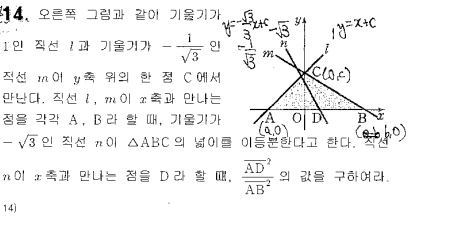
1번은
C를 (0,c) D를(d,0) 으로 놓으면 A와 B와 P (n과 l 의 교점)를 c와 d로 나타낼 수 있습니다. 그러면 ABC넓이 x 1/2 = APD넓이 라는 방정식을 세울 수 있습니다. ( c와 d로 이루어진 방정식 이겠죠? ) 또한 C를 (0,c) D를(d,0) 으로 놓으면 길이 AD와 AB를 c와 d로 나타낼 수 있습니다. 문제에서 주어진 AD^2/AB^2 를 c와 d로 나타내보면 위에서 세운 방정식으로 그 값을 구할 수 있답니다 더 쉬운 풀이가 있을 수도 있겠지만.. 저는 이렇게 풀었답니다. 2번은 기역과 리을이 고민이시라면 기역과 리을 두 그림을 겹쳐서 생각해보시면 삼각 부등식에 의해 기역이 더 짧다는 사실을 알 수 있을 것 같습니다.
10/09/24 08:02
저는 약간 다르게 풀어봤는데, a,b를 c로 표현하는거까진 똑같습니다.
직선 L과 n의 교점을 K라두고 거기서 x축에 수선의 발을 내려서 L라고 두었습니다. 그림으로 보면 간단한데 말로 설명하려니까 복잡해지는데, 직선 AL의 길이와 직선 KL의 길이는 같습니다(기울기가 1인 직선위의 점), 그런데 KL의 길이는 LD의 길이의 루트3배이죠. 삼각형의 각도가 30 60 90일때 대변의 비가 1:루트3:2인걸 이용하면 말이죠. 그럼 AL의 길이와 LD의 길이의 비를 알 수 있습니다. 편의상 LD의 길이를 h라고 두면 AL은 루트3*h 죠. KL의길이도 마찬가지구요. 그럼 삼각형 KAD의 넓이를 h로 표현할 수 있습니다. 이 삼각형의 넓이가 ABC넓이의 1/2인데, 삼각형 ABC의 넓이를 c로 표현한다음 1/2한것이 KAD의 넓이와 같은것을 이용하면 절묘하게 약분이 되면서 c와 h의 비가 구해집니다.(정확하게는 제곱끼리의 비가 구해지죠) 근데 문제에서 묻는것을 c와 h로 나타내보면 결국 이 둘의 비를 묻는것과 같은결과가 된다는걸 알 수 있네요. 휴 생활패턴좀 바꿔본다고 밤새고 하루 버티고 저녁에 잘생각으로 밤을 샜더니 영 어지럽네요. 혹시 말도안되는 풀이였다는 오류가 발생한다면 ㅠㅠ 근데 이렇게 풀어보니 답이 1/2루트3 이 나오는데....;;
10/09/24 08:38
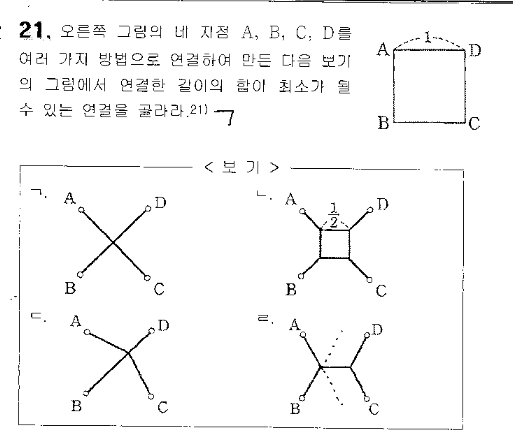
두 번째 문제는 널리 알려진 문제입니다. 네 지점을 잇는 최단경로가 ㉣경로 입니다.
참고로 ㉠경로는 2루트2, 약 2.828이고 ㉣경로는 1+루트3, 약 2.732입니다. ㉣경로의 길이는 보이는 모든 각을 120도로 두고 길이를 계산할 수 있습니다.
|
||||||||||||||