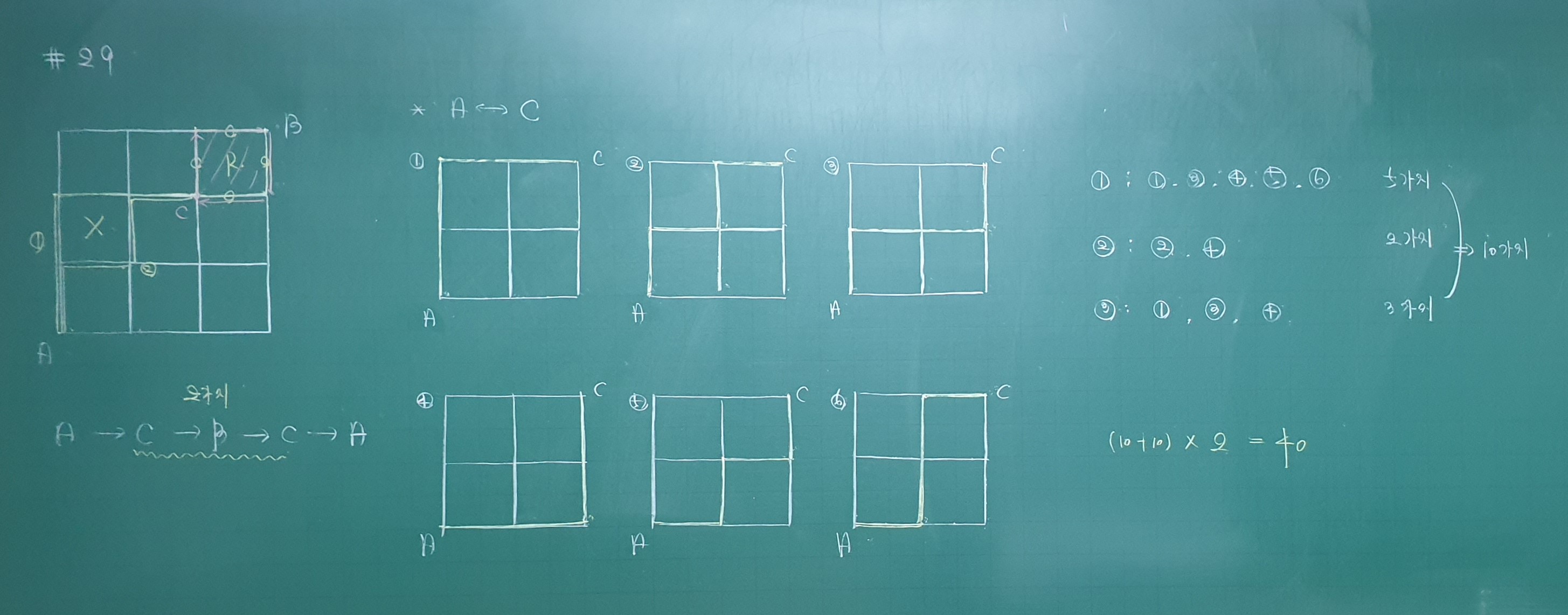|
:: 게시판
:: 이전 게시판
|
- 모두가 건전하게 즐길 수 있는 유머글을 올려주세요.
- 유게에서는 정치/종교 관련 등 논란성 글 및 개인 비방은 금지되어 있습니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
20/05/23 18:22
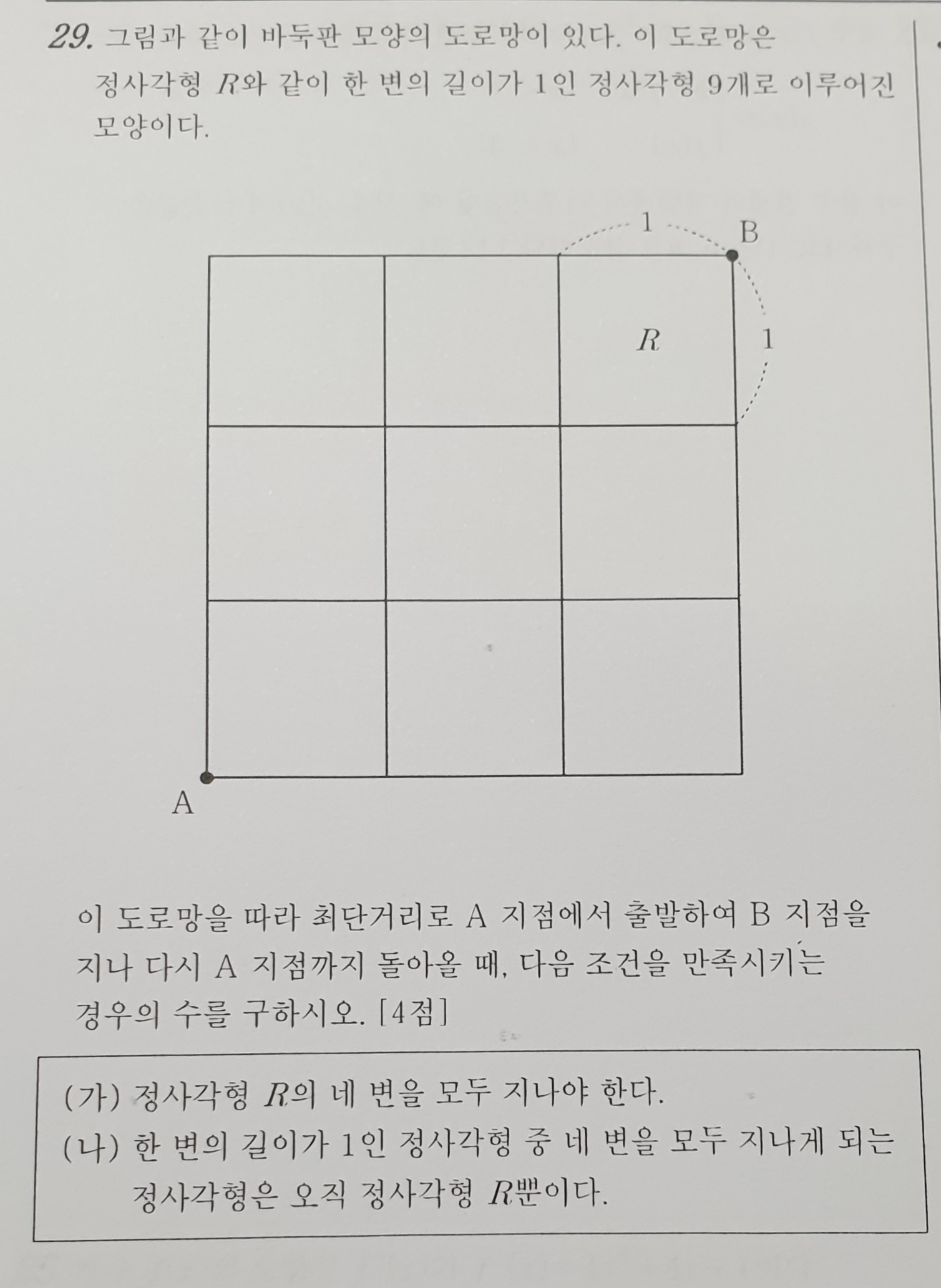
A에서 R왼쪽아래까지 도달했다가 돌아가는 경우의 수를 구해서 X2 하면 되는거 아닌가요 (...)?
수학 푼지 오래되서 내가 너무 쉽게 생각했나?
20/05/23 18:48
(수정됨) 2*(36-2-2-8-8+4)=40
R주위 돌아가는 가지수 2개 2*2 왕복하는 수 36개 2*2에서 왼쪽위나 오른쪽 아래 사각형 모든 변을 지나며 왕복하는 수 각각 2개 2*2에서 오른쪽 위나 왼쪽 아래 사각형 모든 변을 지나며 왕복하는 수 각각 8개 2*2에서 오른쪽 위, 왼쪽 아래 두사각형의 모든 변을 지나는 중복된수 4개
20/05/23 18:51
r 좌하단을 c라고 놓을때 a->c 6가지이고 c->b로 가는 방법이 2가지인데 한번 들어가면 반대길로 나와야 하니까 나오는 루트는 고정 그리고 다시 c->a까지 6가지니까 6*2*6 같기는 한데 잘 모르겠네요
20/05/23 18:53
최단거리라고 했으나 R 의 좌하단 은 무조건 지나가야 하고
A 에서 R 까지 6개 R 에서 B, B 에서 R 까지 2가지 R 에서 A 까지 5개 중 처음간길 빼면 5가지 라서 6*2*5 해서 60 아닐까요
20/05/23 19:03
2 x (5 + 2 + 3) x 2= 40 입니다.
처음 2는 작은 사각형 나중 2는 큰 사각형을 가는 경우의 수가 6가지인데 2개씩 대칭이어서 3가지 경우를 직접 세어보고 2배 한겁니다.
20/05/24 11:59
(수정됨) A까지 가는 길을 6가지로 분류 대칭 이용해서
같은길로 돌아오는 경우 포함 (5+2+3) X 2 = A까지 사각형없이 가는 경우. AB 찍턴은 2가지 경우의 수만 존재하니 20 X 2 = 40
|
||||||||||||||||